Universidade Federal de Pernambuco
Área II - CIn
Projeto de Cálculo Numérico
Setembro/2011
QUESTÃO
Sistemas de Equações Lineares
Construa um programa que dado um sistema de n equações lineares com n variáveis, resolve-o, isto é, encontra o vetor-solução n x 1 que satisfaz simultaneamente todas as suas equações, de acordo com as especificações a seguir:
- O usuário deverá entrar com a matriz n x n de coeficientes aij, bem como o vetor bi (isto é, o sistema é
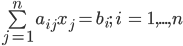 ).
). - O usuário deverá escolher se quer resolver o sistema utilizando:
- O método de Gauss-Jordan sem pivotação
- O método de Gauss-Jordan com pivotação parcial
- O método de Jacobi
- O método de Gauss-Seidel
- Todos os métodos anteriormente listados
- Caso o usuário escolha as opções c., d. ou e. acima, ele poderá ainda fornecer o vetor n x 1 que será usado como aproximação inicial. Caso não o faça, o programa deverá utilizar o vetor nulo como aproximação inicial. Ainda no caso do usuário escolher as opções c., d. ou e., ele poderá ainda fornecer um valor
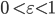 que será utilizado como critério de parada (o programa irá parar quando
que será utilizado como critério de parada (o programa irá parar quando 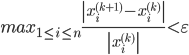 ), e também poderá fornecer o número máximo de iterações M que o programa deverá adotar. Caso esses dois últimos valores não forem fornecidos, o programa deverá usar
), e também poderá fornecer o número máximo de iterações M que o programa deverá adotar. Caso esses dois últimos valores não forem fornecidos, o programa deverá usar 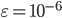 e M = 1.000.
e M = 1.000. - Em todos os métodos deverá ser verificado se o mesmo pode ser aplicado diretamente no sistema fornecido antes de fazê-lo. No caso dos métodos iterativos, só será exigida a verificação da condição da diagonal estritamente dominante. Caso o sistema só possa ser resolvido após a realização de operações básicas que não alteram sua solução, tais como a troca da posição de linhas ou colunas, isso deverá ser feito antes de aplicar o método. No caso dos métodos iterativos, mesmo que não tenha sido possível estabelecer uma configuração em que a convergência esteja garantida, execute o método, encontre uma “solução” e avise ao usuário sobre a confirmação ou não da condição de convergência.
- O programa deverá ser capaz de resolver sistemas com n entre 1 e 50 e utilizar precisão dupla.
- O programa deverá exibir o vetor-solução com 8 casas decimais, utilizando o arredondamento padrão. Também deverá ser exibido o sistema resolvido (que poderá ser idêntico ao fornecido como entrada ou ser uma transformação que não altera a solução do sistema fornecido, caso tal transformação tenha sido necessária).
- Pode ser utilizada qualquer linguagem de programação cujo programa resultante possa ser executado nos computadores do Laboratório de Cálculo Numérico/Computação da Área II. No entanto não será aceita a utilização de funções prontas que implementem os métodos em questão, ou etapas fundamentais desses.
Observações
- Por equipes de até 5 (cinco) alunos pré-formadas;
- A equipe deverá entregar: um CD com o programa auto-executável, o programa fonte (código); uma listagem impressa do programa fonte contido nele, bem como um texto (Modelo do Relatório do Projeto: http://www.cin.ufpe.br/~if215/Projeto/modelo.doc) descrevendo o problema proposto, a solução encontrada, orientações de uso do “software” e comentários sobre as limitações do mesmo;
- Data da entrega do projeto: 1a. aula após o primeiro exercício escolar da disciplina.
- Local para a defesa do projeto: Laboratório de Cálculo Numérico/Computação da Área II. Datas para a defesa do Projeto: a ser definida;
- A nota do projeto será a média aritmética das notas atribuídas à sua correção objetiva e a da defesa do estudante sorteado para representar a equipe;
- O CD e a listagem do programa não serão devolvidos.
Bibliografia
- Métodos Numéricos – J. D. Santos & Z. C. Silva, Editora Universitária - UFPE, 3 a Ed. - 2010.
- Cálculo Numérico - Aspectos teóricos e computacionais, Ruggiero & Lopes, Ed. Makron Book, 2 a Ed. - 1997.
Inscrição: http://www.cin.ufpe.br/~if215/Projeto/Inscricao.doc
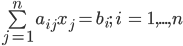 ).
).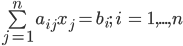 ).
).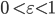 que será utilizado como critério de parada (o programa irá parar quando
que será utilizado como critério de parada (o programa irá parar quando 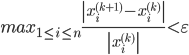 ), e também poderá fornecer o número máximo de iterações M que o programa deverá adotar. Caso esses dois últimos valores não forem fornecidos, o programa deverá usar
), e também poderá fornecer o número máximo de iterações M que o programa deverá adotar. Caso esses dois últimos valores não forem fornecidos, o programa deverá usar 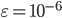 e M = 1.000.
e M = 1.000.