Description of the study

The indicator function of the set A is defined as:

For , a real positive number, we call the cummulative distribution of a Rayleigh random variable with parameter the function defined by

It is easy to see that has a density given by

If Y is a random variable with distribution , then

Then

Let n be a positive integer and .

 

 

We could use stochastic simulation to study the behaviour of different estimation procedures (to be defined) of the parameter , under several situations of the pure model (varying and n) and of the contaminated model (varying , , , , and n). Thus, gaining some knowledge about the robustness of these procedures.

As we said before, a study like this has practical relevance since, as is usually the case in applications, we might not be sure about the pureness of the distribution of the observations (in fact the contaminated model is the most frequent case). But the reader must keep in mind that this a mere example within this work, just aiming at showing how the suggestions presented in the previous Sections could be applied. Therefore, we shall restrict this study to a quite preliminar stage, ending this paper with some guidelines for its continuation.

The pure model will be studied for the following situations: and n(i)=100i for . The contaminated model will be studied for the following cases: n(i)=100i for , , , and . Without loss of generality, we can suppose that every outcome of the random vector , with n any of the n(i) above, will satisfy the following two conditions:

We will consider the following estimation procedures for based in :

1. The ML estimator of defined by

   

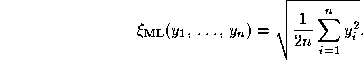
   This is the maximum likelyhood estimator of , under the pure model.

2. The MO estimator of defined by

   

   This is the estimator of based on the first sample moment, under the pure model.

3. The TML estimator of defined by

   

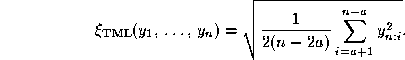
   This is the trimmed ML estimator of with a proportion of deleted observations equal to .

4. The T estimator of defined by

   

   This is the trimmed mean estimator of with a proportion of deleted observations equal to . In both trimmed estimators we wrote and denotes the vector sorted in ascending order. The trimmed observations are the smallest and the biggest ones.

5. The MAD estimator of (Bustos, 1981) defined by

   

   where , and K=.4485. This is the Median Absolute Deviation estimator of , with the correction constant, K, determined using numerical tools.