3 - Função Hashing não-trivial

Considere um tabuleiro do jogo do 8:



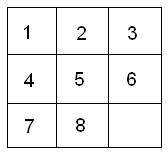
Essa questão tem como objetivo principal a indexação direta desses tabuleiros.
O problema é encontrar um função Hashing para essas seqüências de tal forma que,
Para todos índices i1, i2: i1 < i2 se T1 < T2 (e não poderá haver colisões).
T1 < T2 se só se F(T1) < F(T2).
F(T) = T₁₁T₁₂T₁₃T₂₁T₂₂T₂₃T₃₁T₃₂T₃₃
Considere a casa vazia como o valor 0.
OBS: Se se preencher todo o array com os tabuleiros, deveremos ter no máximo
9! posições alocadas... o tamanho do array NÃO deve ultrapassar 9!, isso significa
que sua função hash deve mapear os 9! tabuleiros em inteiros de 0..(9!-1).
            Chamaremos essa função de HASH(T).

Entrada e Saída de dados

0 1 2

3 4 5

6 7 8



0 1 2

3 4 5

6 8 7



0 1 2

3 4 5

7 6 8



8 7 6

5 4 3

2 1 0

Saída correspondente

0

1

2

362879