1. Com certeza, você já passou pela experiência na qual, quando muitas pesssoas estão usando a Internet simultaneamente, a rede torna-se muito, mas muito lenta. Para dar um fim a este problema, o CIn-UFPE desenvolveu um método para resolver tal contingência nos horários de pico, cortando o acesso à rede de algumas cidades de maneira justa e sistemática.

As cidades brasileiras foram numeradas aleatoriamente de 1 a n: São Paulo foi a número 1, Recife número 2, Salvador número 3, e assim por diante. Então um número m seria escolhido randomicamente, e a primeira cidade a ter o acesso à rede cortado seria a número 1 (claramente, nada mais justo).

Em seguida o mesmo aconteceria para cada m-ésima cidade após ela, voltando ao inicio após o n e ignorado as cidades que já estão sem rede. Por exemplo, para n=17 e m=5, o acesso seria cortado na seguinte ordem:

[ 1, 6, 11, 16, 5, 12, 2, 9, 17, 10, 4, 15, 14, 3, 8, 13, 7 ]

O problema seria cortar a rede de Recife por último (afinal, é de lá que vêm os melhores programadores). Por isso, para um dado n, é necessário escolher o valor de m cuidadosamente, para que a cidade 2 seja a última escolhida.

Seu trabalho é escrever um programa que determine, para um dado número de cidades, o menor valor de m que garanta que Recife possa navegar na web enquanto o resto das cidades está sem rede.

2. Escreva um programa que, dados dois polinômios na forma ∑c_ixⁱ, encontre o polinômio resultante de sua soma.

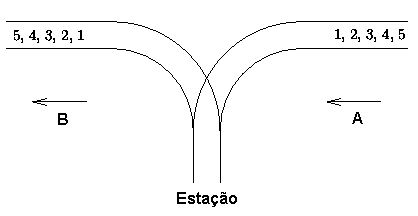
3. Há uma famosa estação numa estrada de ferro na Cidade PushPop. O relevo da cidade é bastante acidentado, e a estação foi construída no século passado. Infelizmente, as verbas eram limitadas naquela época, por isso a estação só podia ter uma saída (veja a figura abaixo). Devido à falta de espaço disponível, ela só podia ter um trilho.