Séries de Fourier

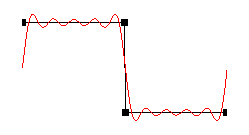
A transformada de Fourier desempenha um papel de grande importância em vários ramos das ciências exatas. As séries de Fourier são um caso particular da transformada de Fourier e permitem decompor uma função périódica qualquer na soma de um número infinito de funções senoidais com diferentes frequências e amplitudes. Além de poder ser empregado diretamente em um grande número de problemas, o estudo das séries de Fourier é uma introdução bastante conveniente a outro caso particular da transformada de Fourier: a transformada discreta de Fourier. Esta última está diretamente associada ao processamento digital de sinais pois existem algoritmos capazes de computá-la com grande eficiência.

Com o intuito de tornar o aprendizado das séries de Fourier acessível a um público com menor maturidade matemática foi desenvolvida uma ferramenta que permite ao estudante definir uma função a partir de um conjunto de funções lineares e visualizar a aproximação desta função pela sua série de Fourier e os termos da série. Esta funcionalidade permite que o estudante adquira uma noção intuitiva do comportamento dos termos da série de fourier de uma determinada função.