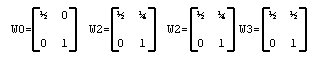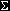A aplicação de autômatos para imagens em grayscale(escala em tonalidades de cinza), utiliza-se números reais para a representação de cada cor. Esses números têm uma variação de 0 a 2^k, onde k é, geralmente, 8.Temos então uma função f:^m -> R para definir o endereço dos pixels e uma outra função que define a imagem de multi- resolução g: 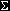^*->R.

No entanto é exigido uma certa compatibilidade de resolução. Isso é possível através da utilização de funções com preservação de média. As funções seguem a seguinte relação:

f(w) = ¼[f(w0) + f(w1) + f(w2) + f(w3)]   
,para qualquer w R^*.
Essas funções são chamadas de ap-functions (average preserving functions) ou funções que preservam a média. Aqui chamaremos de funções PM. As operações de soma e multplicação são definidas abaixo:

(f1 +f2)(w) = f(w1) + f(w2),
para qualquer f1,f2:^*->R e w ^*;
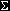(cf)(w) = cf(w),
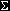para qualquer função f: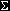^*->R e para um número real c
É importante ressaltar que qualquer combinação de funções PM formam um outra função PM.

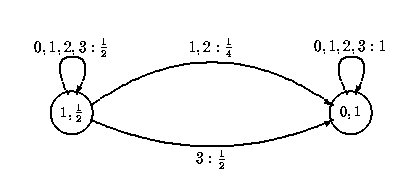
A representação de uma imagem em grayscale é feita através de AFPs - autômatos finitos de m estados com peso(m-state weighted finite automaton ou WFA). Esses autômatos são representados de maneira similar a dos AFD. Cada estado é representado por um círculo e os estados final e inicial são postos em círculos também. Os WFA diferem dos AFD por possuírem pesos em suas arestas. Um autômato pode ser definido pelos seguintes componenentes:
- Um vetor linha I^a R^1xm(representando a distribuição inicial);
- Um vetor coluna F^a R^mx1(representando a distribuição final);
- Matrizes de peso W^A_a R^mxm para todo a que pertence a .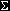

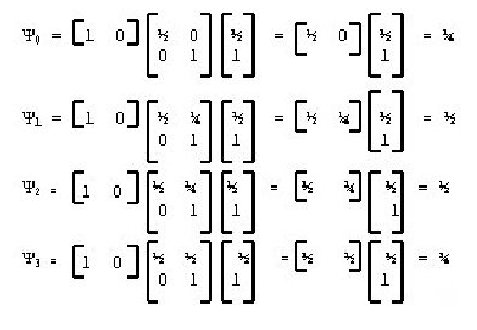
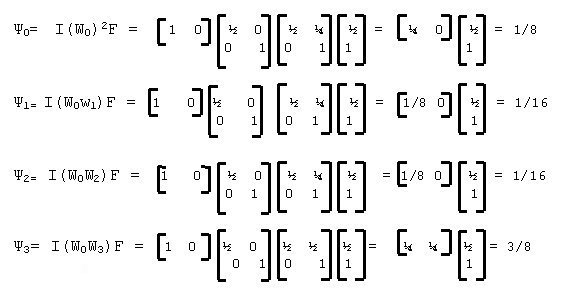
As matrizes irão indicar as cores de cada pixel de acordo com seu posicionamento. Cada endereço ou palavra do pixel seguirá um caminho no autômato que dará a sua cor específica. Quanto mais próxima de 0 mais escura será a tonalidade de cinza. Quando próxima de 1 mais clara ela será. Um exemplo de cálculo de tonalidade para pixels será dado abaixo:

Considere um AFP A com alfabeto 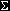= 0,1,2,3, com distribuição inicial I = (1,0), distribuição final F = (1/2,1), e as seguintes matrizes de peso:

Considere, também, as figuras:

O autômato que representa a imagem é mostrado abaixo:

Exemplo de resolução para a figura A:

Exemplo de resolução para o quadrante 0 da figura A:

Zoom:Para recuperar uma subimagem de uma imagem codificada por um AFP precisamos usar a seguinte função:

f_u(w) = f(uw), para todo w ^*
onde devemos definir que f é uma imagem arbitrária de multiresolução sobre e u ^*. É preciso também esclarecer que f_u é uma imagem originada de f por um zoom de um subquadrado de endereço u.

Decodificador:para decodificar uma imagem de resolução de 2^kx2^k nós computamos, para todos os endereços em {0,1,2,3}^k, f_A(a1a2...ak)=I^AW^A_a1W^A_a2...W^A_ak