NetBook - Tutorial

1. Visão Geral

            NetBook contém quatro módulos:

·        Estatística – Neste módulo estão todos os procedimentos estatísticos.

·        Geração – É possível com NetBook gerar variáveis aleatórias e tráfego. Estas simulações são o conteúdo deste módulo.

·        Transformação – Módulo responsável pela transformação de dados.

·        Gráfico – Este módulo contém apenas gráficos.

            A Figura 1 mostra a tela inicial de NetBook.

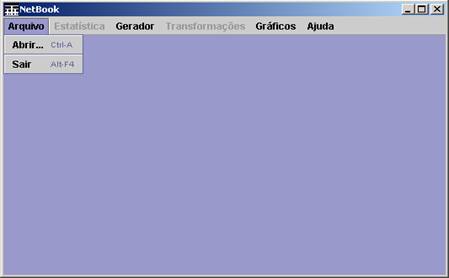
Figura 1. Tela Principal

2. Abrir um arquivo de dados

            A entrada dos dados no NetBook é feita por meio de arquivos de texto, com extensão txt, dat ou log, ou arquivos do Microsoft Excel (cuja extensão é xls). Os arquivos podem ser constituídos por várias colunas de dados, porém, para os cálculos estatísticos, deve-se sempre selecionar uma coluna. Além disso, o arquivo só deve conter valores numéricos (inteiros ou reais).

            Para selecionar um arquivo com os dados a serem analizados, clique em Arquivo no menu principal e depois em Abrir. Uma janela se abrirá para que você selecione o arquivo.

            A Figura 2 mostra um exemplo de arquivo de entrada.

Figura 2. Exemplo de um Arquivo de Entrada

            É possível abrir mais de um arquivo ao mesmo tempo. Cada arquivo aberto estará associado a uma janela interna do programa.

3. Estatística

            Para utilizar um dos procedimentos do módulo Estatística, basta selecionar a janela correspondente ao arquivo que contém os dados desejados e em seguida escolher a opção do menu Estatística apropriada. Antes da realização da maioria dos procedimentos, será msotrada ao usuário a tela mostrada na Figura 3, que permitirá a escolha da coluna e do intervalo de linhas que devem ser usadas.

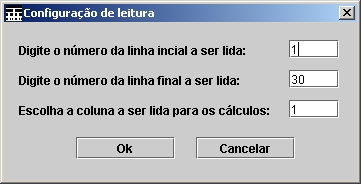
Figura 3. Diálogo para escolha do conjunto de dados a ser usado

O resultado dos cálculos será mostrado na janela interna correspondente ao arquivo de dados usado.

3.1. Medidas de Tendência Central

            O primeiro ítem do menu Estatística é o sub-menu Medidas de Tendência Central. Nele estão presentes os seguintes ítens: Média, Mediana e  Moda.

3.2. Medidas de Dispersão

            O segundo ítem se refere a Medidas de Dispersão. Nele encontra-se as opções para calcular Amplitude, Coeficiente de Variação, Desvio Padrão e Variância. Quando a opção Amplitude for escolhida, será mostrado também os valores mínimo e máximo.

3.3. Separatrizes

            O terceiro ítem do menu Estatística permite o cálculo de Separatrizes. A tela mostrada na Figura 4 será mostrada, para permitir a escolha da separatriz desejada.

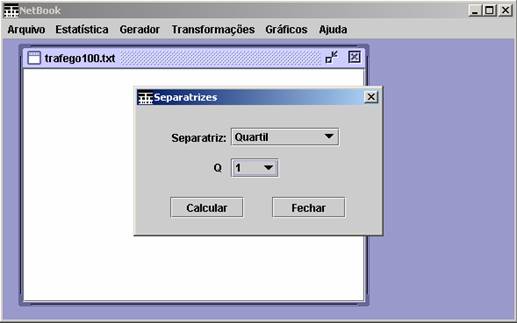
Figura 4. Cálculo das Separatrizes

3.4. Autocorrelações

            Para calcular as autocorrelações deve-se clicar no menu Estatística e em seguida escolher a opção Autocorrelações. Isso abrirá a janela mostrada na Figura 5. Essa janela permite escolher qual coluna do arquivo de dados será usada para o cálculo das autocorrelações. É possível também escolher a linha inicial e a linha final de um subconjunto da coluna escolhida com o qual se deseja trabalhar. Os valores sugeridos pela janela para esse campo são a primeira e a última linha, ou seja, toda a coluna.

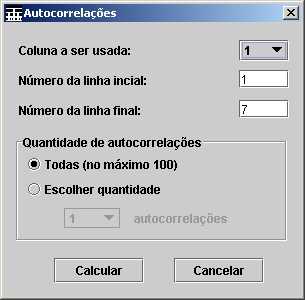
Figura 5. Diálogo usado para o cálculo de autocorrelações

3.5. Inferência

            O sub-menu Inferência permite a realização de testes de bondade de ajuste, estimação do parâmetro de Hurst e do parâmetro da distribuição de Pareto. Dois diferentes testes de bondade de ajuste estão disponíveis no sub-manu Teste de Bondade de Ajuste. O primeiro é o Kolmogorov-Smirnov. Após escolher o conjunto de dados usado deve-se escolher a distribuição e o nível de significância que serão usados no teste. Essas escolhas são feitas através da nova tela que se abrirá, mostrada na Figura 6.

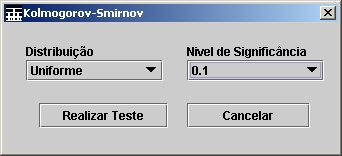
Figura 6. Escolha da distribuição e do nível de significância

            Por fim, o resultado do teste é mostrado na tela referente ao arquivo contendo os dados testados, como mostrado na Figura 7.

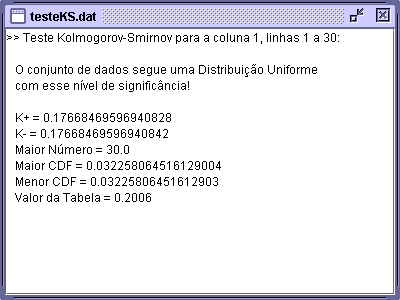
Figura 7. Resultado do teste Kolmogorov-Smirnov

            O segundo teste de bondade de ajuste disponível é o Qui-Quadrado. Ao selecionar esse ítem será pedido para escolher o conjunto de dados a ser utilizado e em seguida, a tela mostrada na Figura 8 será disponibilizada, através da qual é possível a escolha do grau de liberdade, da distribuição e do nível de significância usados.

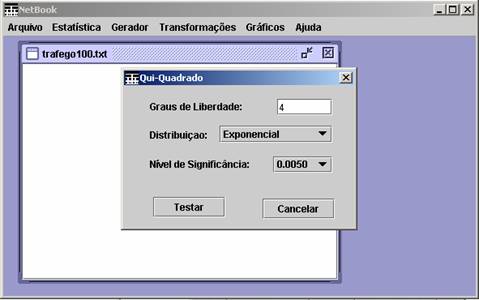
Figura 8. Tela para realização do teste Qui-Quadrado

            Para estimar o parâmetro de Hurst ou o parâmetro da Pareto, basta selecionar os itens Parâmetro de Hurst ou Parâmetro da Pareto respectivamente.

4. Geradores

            Para permitir ser usado e testado sem que o usuário disponha de dados reais coletados de uma rede de computadores, NetBook possui dois módulos que geram arquivos texto contendo uma coluna de dados pseudo-randômicos. O primeiro gera valores que seguem uma dada distribuição, enquanto o segundo gera conjuntos de dados que representam o tráfego de uma rede de computadores.

4.1. Gerador de Variáveis Aleatórias

            Para gerar valores aleatórios que seguem uma distribuição exponencial o usuário deve clicar no menu Gerador, escolher o sub-menu Variáveis Aleatórias e em seguida escolher a opção Exponencial. A Figura 9 mostra a tela que aparecerá para permitir a escolha dos parâmetros do gerador congro-linear, a quantidade de números que devem ser gerados e o parâmetro  da distribuição.

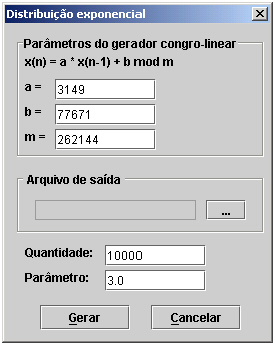
Figura 9. Geração de uma variável aleatória exponencial

            Devem ser escolhidos também o nome e o caminho do arquivo que será gerado contendo os dados agregados. Para escolher o arquivo deve-se apertar no botão localizado na área de escolha do arquivo de saída. Caso o arquivo escolhido ainda não exista, o mesmo será criado automaticamente por NetBook e uma mensagem, informando a criação, será mostrada ao usuário.

            Para gerar valores aleatórios que seguem uma distribuição de Pareto o usuário deve clicar no menu Gerador, escolher o sub-menu Variáveis Aleatórias e em seguida escolher a opção Pareto. A Figura 10 mostra a tela que aparecerá para permitir a escolha dos parâmetros do gerador congro-linear, a quantidade de números que devem ser gerados e o parâmetro da distribuição.

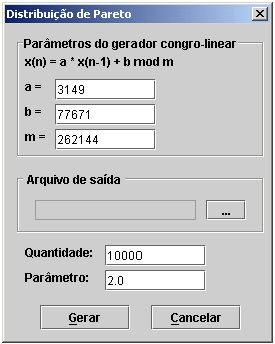
Figura 10. Geração de uma variável aleatória que segue uma distribuição de Pareto

            Não deve ser esquecido de escolher o arquivo de saída, como feito na geração de uma variável que seguem uma distribuição exponencial.

4.2 Gerador de Tráfego

            Clicando no sub-menu Tráfego será aberta a tela mostrada na Figura 11. Esta tela permite a escolha da quantidade de observações desejadas (o equivalente à quantidade de segundos durante a qual a “coleta” será realizada) e a escolha da banda passante do link. Além disso, deve-se também escolher o arquivo onde o tráfego gerado deve ser salvo.

 

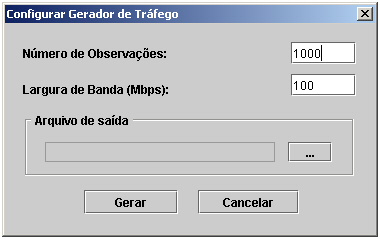
Figura 11. Geração de Tráfego

5. Transformações

            Nesta versão, o NetBook apenas faz agregação de um conjunto de dados. Outras transformações serão implementadas em versões posteriores.

5.1. Agregação

            Para gerar um conjunto de dados agregados, deve utilizar o menu Transformações e em seguida escolher a opção Agregação. Isso abrirá a tela mostrada na Figura 12.

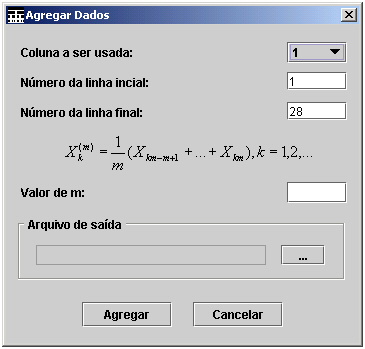
Figura 12. Escolha dos parâmetros da agregação

            Os três primeiros campos dessa tela se referem à escolha do conjunto de dados que será agregado. Após a fórmula da agregação, é mostrado um campo onde deve ser digitado o valor de . Esse valor indica de quantos em quantos valores o conjunto de dados deve ser agregado. Por fim, é mostrado ao usuário um campo que conterá o nome e o caminho do arquivo que será gerado contendo os dados agregados. Para escolher o arquivo deve-se apertar no botão mostrado ao lado desse campo. Caso o arquivo escolhido ainda não exista, o mesmo será criado automaticamente por NetBook e uma mensagem, informando a criação, será mostrada ao usuário.

            A implementação de NetBook para a agregação segue a fórmula

.

O conjunto, por exemplo, consiste de

.

Um fato que deve ser observado é que os últimos elementos são descartados caso a quantidade de elementos do conjunto de dados não seja um múltiplo de . No exemplo acima, por exemplo, se o conjunto de dados contiver oito elementos,  e  seriam descartados.

6. Gráficos

            Os gráficos disponíveis em NetBook podem ser agrupados em duas categorias: gráficos gerados a partir de um arquivo de dados e gráficos gerados a partir de uma função de uma variável.

6.1 Gráficos gerados a partir de um arquivo de dados

Sete tipos de gráficos podem ser gerados a partir dos dados contidos em um arquivo de entrada:

• diagrama de dispersão ou gráfico de pontos;
• gráfico de linhas;
• gráfico de linhas e pontos;
• gráfico de freqüências;
• gráfico escada;
• correlograma;
• gráfico texturizado;
• gráfico da função de distribuição acumulada;
• CD-Plot.

            Cada um contém características específicas, as quais serão posteriormente explicadas.

            Para gerar gráficos nesta categoria deve-se clicar no menu Gráficos e em seguida escolher a opção Plotar dados, ou utilizar as teclas de atalho Ctrl + G. Isso abrirá a janela mostrada na Figura 13, através da qual o usuário escolhe o gráfico a ser gerado e suas características.

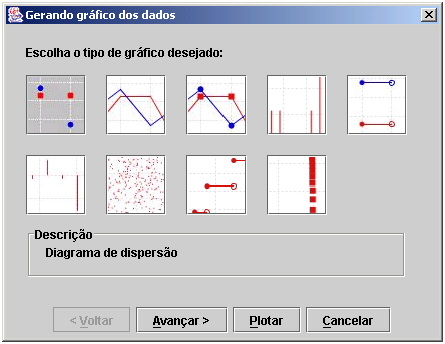
Figura 13. Escolha do tipo do gráfico de dados

            A primeira escolha a ser feita é o quanto ao tipo do gráfico. Para isso o usuário deve clicar em uma das sete figuras, cada uma indicando um dos tipos acima citados, e em seguida clicar no botão avançar para seguir adiante no processo de geração. A segunda etapa da geração diz respeito aos dados que serão usados pelo gráfico. Como esta etapa depende de tipo de gráfico que foi escolhido, ela será explicada junto com a descrição de cada um dos tipos. Seguindo o processo novamente através do botão avançar é dada a opção ao usuário de escolher o título do gráfico e o nome dos eixos vertical e horizontal, Figura 14.

 

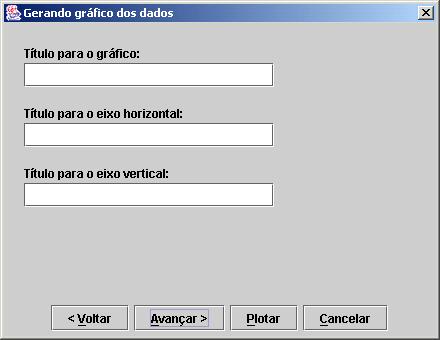
Figura 14. Escolha dos títulos do gráfico

            Por fim, na última tela o usuário pode escolher a presença ou não da legenda, de tooltips e de linhas de grade, Figura 15 Em qualquer uma das etapas o usuário pode escolher plotar o gráfico sem antes passar pelas etapas restantes. Acontecendo isso, o NetBook usará as opções padrões de cada tipo de gráfico.

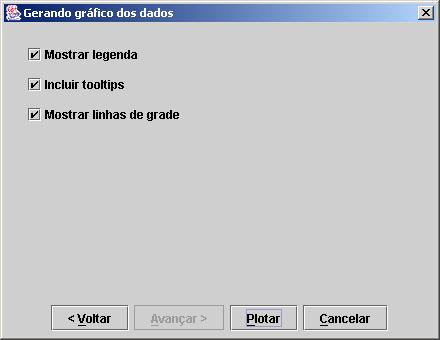
Figura 15. Escolha dos atributos do gráfico

6.1.1. Diagrama de Dispersão ou Gráfico de Pontos

A primeira opção de gráfico que pode ser gerado a partir dos dados do arquivo de entrada é o diagrama de dispersão, ou seja, um gráfico formado por pontos no plano cartesiano. Com esta opção é possível gerar gráficos com mais de um conjunto de dados, sendo os pontos de cada conjunto representado por um símbolos e uma cor diferente dos demais. A escolha dos conjuntos de dados é feita na segunda etapa da geração, ou seja, após ter sido escolhido o tipo do gráfico.

            Nesta etapa, Figura 16, o usuário deve primeiro escolher se o eixo horizontal será formado pelos números naturais, N = {0, 1, ..., n, ...}, ou por uma coluna específica do arquivo de dados.

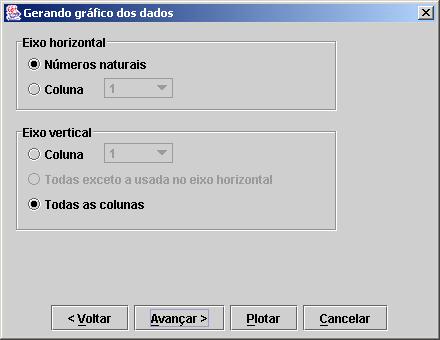
Figura 16. Escolha dos conjuntos de dados para o diagrama de dispersão, gráfico de linhas e gráfico de linhas e pontos.

            Caso tenha escolhido utilizar os números naturais, o usuário poderá escolher para o eixo vertical utilizar um conjunto de dados apenas, cujos valores serão obtidos de uma coluna específica, ou vários conjuntos de dados, cujos valores serão obtidos de cada uma das colunas do arquivo de entrada. Tendo escolhido utilizar uma coluna específica para o eixo horizontal, além das duas opções citadas anteriormente, é dada a opção de gerar um conjunto de dados para cada coluna do arquivo excetuando-se a utilizada para o eixo horizontal. A Figura 17 mostra um exemplo desse tipo de gráfico.

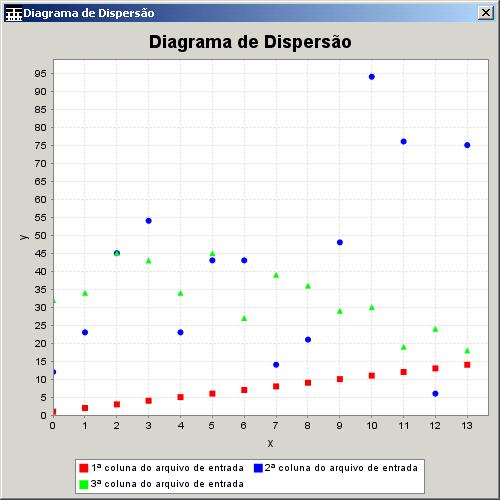
Figura 17. Diagrama de Dispersão

6.1.2. Gráfico de Linhas

Os pontos deste gráfico estão ligados por segmentos de reta e não são marcados por símbolos.

            A Figura 18 mostra um exemplo desse de gráfico. Observa-se que a legenda foi omitida.

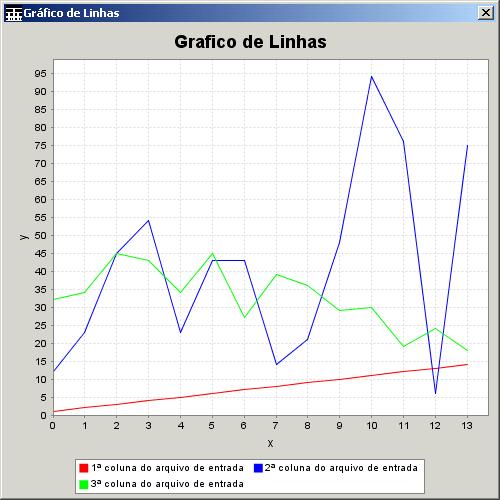
Figura 18. Gráfico de Linhas

6.1.3. Gráfico de Linhas e Pontos

Este tipo de gráfico é uma mistura dos dois anteriores, pois neste os pontos são ligados e marcados por símbolos.

            A Figura 19 mostra um exemplo desse tipo de gráfico. Observe que as linhas de grade foram omitidas na geração desse gráfico.

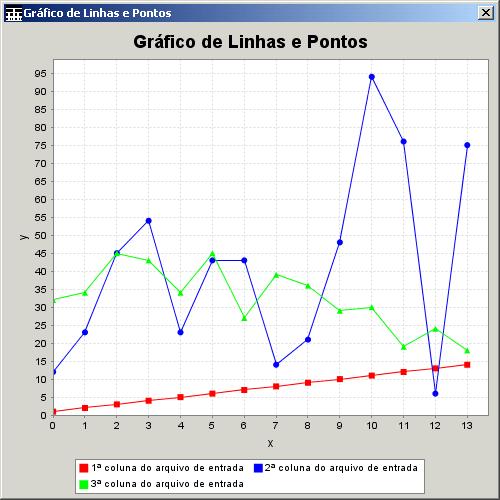
Figura 19. Gráfico de Linhas e Pontos

6.1.4. Gráfico de Freqüências

O gráfico de freqüências tem como objetivo mostrar a freqüência com que cada um dos valores aparece no conjunto de dados. Este gráfico, ao contrário dos anteriores, só permite um conjunto de dados, assim, a escolha inicial é a coluna do arquivo de entrada que será usada, Figura 20. Deve também ser escolhida a forma como a freqüência aparece. A opção padrão é na forma de freqüência relativa, isto é, todos as freqüências pertencem ao intervalo [0, 1]. Esse gráfico pode ser referenciado como gráfico de probabilidades. As outras duas formas são absoluta, onde é mostrado o número de ocorrências de cada valor, e percentual, onde a freqüência aparece em porcentagem. Isto é, supondo-se que  aparece  vezes, ,  vezes, ..., ,  vezes, então, para

freqüência absoluta de x_j = ,

freqüência relativa de x_j = ,

freqüência percentual de x_j = .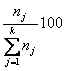

Figura 20. Escolha dos conjuntos de dados para o Gráfico de Freqüências

            Uma outra particularidade deste gráfico é a existência de padrões para o título do gráfico e títulos dos eixos, o que não impossibilita a escolha de um outro por parte do usuário. A Figura 21 mostra um exemplo do gráfico de freqüências usando esses valores padrões.

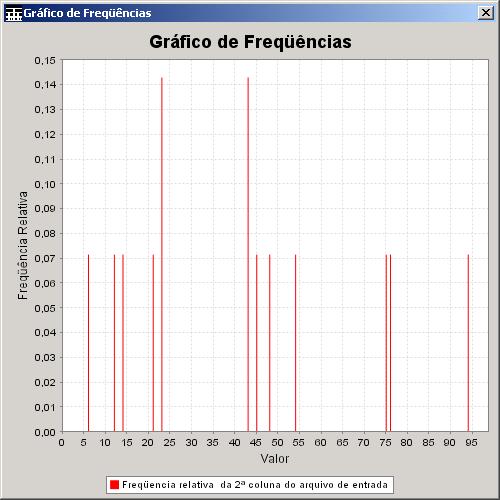
Figura 21. Gráfico de Freqüências

6.1.5. Gráfico Escada

O gráfico escada é mais elaborado que os demais pelo fato de exibir segmentos de retas para intervalos específicos no eixo horizontal. O tamanho dos intervalos pode ser definido de duas formas, Figura 22. Na primeira a amplitude dos intervalos é fixa. Neste caso o usuário deve informar o valor do eixo horizontal onde o primeiro intervalo deve começar e a amplitude dos intervalos. Os demais intervalos começam onde termina o anterior. Na segunda forma, a amplitude dos intervalos é variável. Para isso o usuário deve especificar uma coluna do arquivo de entrada que será usada para delimitar os mesmos. Assim, o primeiro intervalo começa no primeiro valor da coluna escolhida e vai até o segundo valor da mesma coluna. O segundo intervalo começa do segundo valor e vai até o terceiro valor, e assim por diante. Para que os intervalos não se sobreponham a coluna do arquivo de dados escolhida para definir os intervalos deve estar ordenada.

Figura 22. Escolha dos conjuntos de dados para o Gráfico Escada

            Como nos três primeiros gráficos, é possível usar um conjunto de dados para cada coluna do arquivo de entrada (excluindo ou não a coluna usada no eixo horizontal), ou usar apenas um conjunto de dados definido por uma coluna específica.

            A geração de um gráfico escada possui uma etapa a mais que os demais gráficos, Figura 23, onde o usuário pode escolher se os intervalos devem ser abertos a direita ou a esquerda e se os intervalos da extrema esquerda e direita devem seguir para menos infinito e mais infinito respectivamente, como é o caso do exemplo da Figura 24.

Figura 23. Escolha de atributos do Gráfico Escada

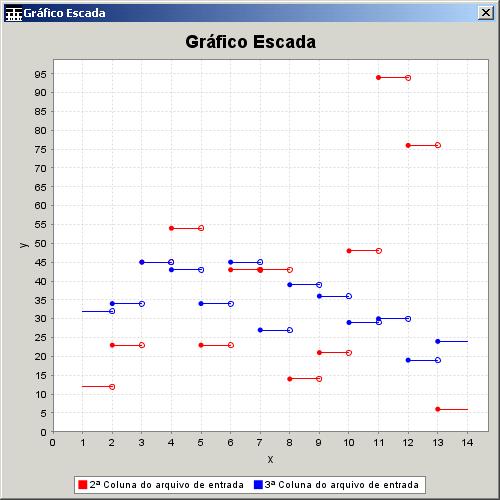
Figura 24. Gráfico Escada

            Neste exemplo a coluna escolhida (1ª coluna) possuía os valores de 1 a 14. A razão para isto é porque este gráfico pode ser usado para exibir as probabilidades da função de distribuição acumulada de variáveis aleatórias discretas unidimensionais, F. O fato dos intervalos serem abertos à direita ou à esquerda diz respeito à definição de F, se

 

6.1.6. Correlograma

O correlograma é uma representação gráfica das autocorrelações de um conjunto de dados. Para gerá-lo, o usuário deve escolher que coluna do arquivo de entrada será usada e a quantidade de autocorrelações que serão mostradas. Existem duas possibilidades para a escolha da quantidade: deixar que o programa mostre todas as autocorrelações posíveis (quantidade de linhas do arquivo – 1), não ultrapassando o limite máximo de 100 autocorrelações, ou especificar a quantidade desejada, Figura 25. Portanto, se o arquivo tem n valores, o número máximo de autocorrelações que NetBook calcula é

.

Figura 25. Escolha dos conjuntos de dados para o Correlograma

            Assim como o gráfico de freqüências, o correlograma também possui padrões para o título e para o nome dos eixos. A Figura 26 mostra um exemplo de correlograma gerado com os valores padrões.

 

Figura 26. Correlograma

3.4.1.7. Gráfico Texturizado

O gráfico texturizado é útil na representação de dados unidimensionais, sendo uma tentativa de mostrar todos os pontos individualmente. Para isso é necessário que os pontos sejam deslocados verticalmente de forma parcialmente randômica e parcialmente definida, o que é feito da seguinte forma. Se existirem 100 ocorrências de um dado valor no conjunto de dados, existirá no gráfico 100 pontos para o dado valor no eixo horizontal, onde cada um deles estará localizado num segmento de tamanho 1/100 do eixo vertical. O ponto exato em que o ponto se localizará dentro do segmento que lhe cabe, será atribuído randomicamente. A Figura 27 mostra um exemplo do gráfico Texturizado.

Figura 27. Gráfico Texturizado

6.1.8 Gráfico da Função de Distribuição Acumulada

NetBook também é capaz de criar o gráfico da função de distribuição acumulada

de forma simples e direta, sem que o usuário precise criar um conjunto de dados específico para ser usado pelo gráfico escada.

            Para gerá-lo, o usuário deve escolher a coluna do arquivo de entrada será usada, o título e o nome dos eixos e a presença ou não da legenda, tooltips e linhas de grade. A Figura 28 mostra um exemplo desse gráfico gerado com os valores padrões para o título e o nome dos eixos.

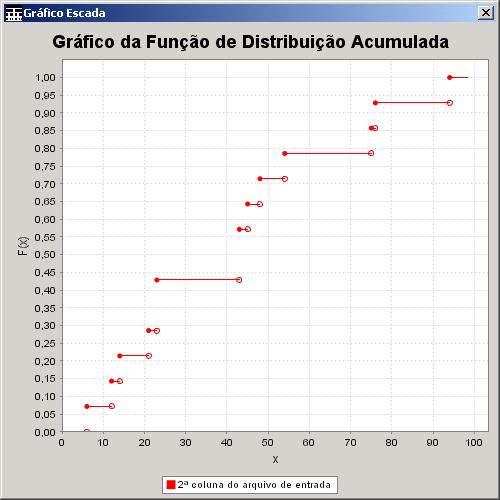
Figura 28. Gráfico da Função de Distribuição Acumulada

3.4.1.9 CD-Plot

O gráfico da distribuição complementar em eixos logaritmos é bastante útil para estimar o parâmetro  de uma distribuição de Pareto, como explicado na seção 3.1.5.3.

            Para gerá-lo, o usuário deve escolher a coluna do arquivo de entrada será usada, o título e o nome dos eixos e a presença ou não da legenda, tooltips e linhas de grade. A Figura 29 mostra um exemplo desse gráfico gerado com os valores padrões para o título e o nome dos eixos.

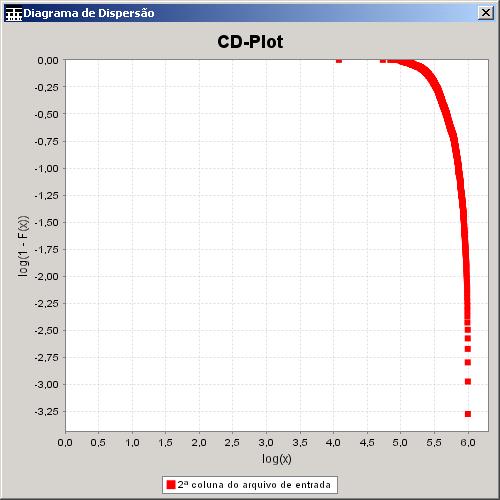
Figura 29. CD-Plot

6.4.2. Gráficos Gerados a Partir de uma Função

Os gráficos de funções podem ser gerados através da opção Plotar função, também do menu Gráficos, ou utilizando as teclas de atalho Ctrl + F.

            Como na geração de um gráfico de dados, uma janela com botões representando tipos de gráficos se abrirá para permitir a escolha do usuário.

            O gráfico de funções lineares e quadráticas, por se tratarem de funções mais comumente usadas, pode ser gerado através do primeiro e segundo botão respectivamente. Nesses casos o usuário só precisará digitar os parâmetros das funções nos campos indicados e escolher o menor e o maior valor de . A Figura 30 mostra a geração do gráfico de uma função linear e a Figura 31 mostra a geração do gráfico de uma função quadrática.

Figura 30. Geração de um gráfico de função linear

Figura 31. Geração de um gráfico de função quadrática

            O terceiro botão dessa janela deve ser usado quando o gráfico desejado for de uma função que nem seja linear nem quadrática. Neste caso o usuário deve entrar com a função no lugar apropriado, como na Figura 32, utilizando a sintaxe da Tabela 1, definida para NetBook.

Tabela 1. Sintaxe definida para NetBook

 

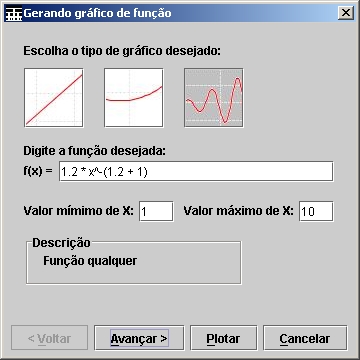
Figura 32. Geração de um gráfico de uma função qualquer

            Além da função, o usuário tem de especificar o domínio da variável .

            Esse tipo de gráfico é útil para a representação da função densidade de variáveis aleatórias unidimensionais contínuas, tais como a normal, exponencial, qui-quadrado, t-Student, Pareto, Weibull e log-normal.

A Figura 33 mostra o gráfico da função densidade da Pareto,

 ,   e  ,

instanciada para  e  variando entre 1 e 10. Neste caso, foi digitado

1.2*x^(1.2 + 1)

no campo da função, 1 no campo de valor mínimo de x e 10 no campo de valor máximo de .

 

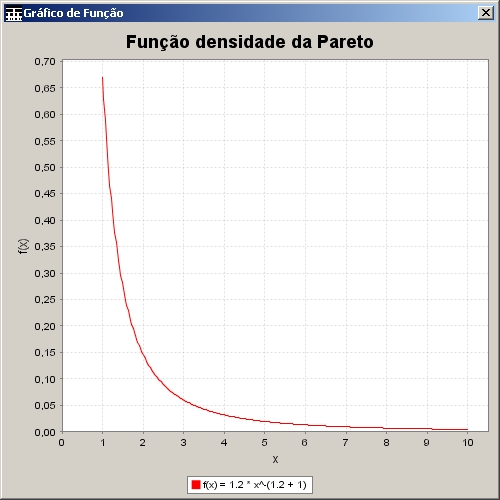
Figura 33. Gráfico da função densidade da Pareto

            As duas últimas etapas da geração de um gráfico de função (escolha dos títulos e atributos) são iguais às do processo de geração do gráfico de um conjunto de dados.

6.3. Outros Gráficos

            O NetBook ainda não suporta a geração de gráficos de funções que apresentam descontinuidades, como por exemplo, o gráfico da função , com  variando de 0 a 10. Isso porque o gráfico é formado a partir da interpolação de 300 pontos, cujos valores são calculados com o auxílio de um interpretador desenvolvido para o NetBook. Caso ocorra, por exemplo, uma divisão por zero durante o cálculo de um dos valores o interpretador retornará o valor infinity, que é então passado para a biblioteca de gráficos usada pela ferramenta, a JfreeChart, resultando assim em uma exceção, pois a biblioteca não suporta gráficos com valores tendendo para infinito. Para que isso não ocorra, o NetBook mostra ao usuário a mensagem da Figura 34.

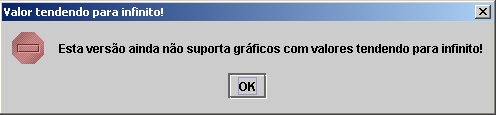
Figura 34. Mensagem de erro na geração de gráficos de funções que apresentam descontinuidades

            É preciso enfatizar que o usuário só recebe a mensagem de erro anteriormente referenciada quando o cálculo do interpretador realmente resultar em infinito. No caso do valor estar presente no gráfico, porém entre dois pontos quaisquer, resultará em um gráfico mal-formado, como é o caso do exemplo da Figura 31.

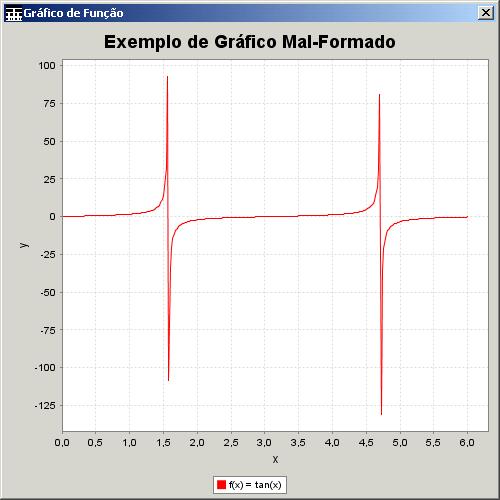
Figura 35. Exemplo de um gráfico mal-formado

7. Dúvidas, Comentários e Sugestões

            Caso alguma dúvida persista após a leitura deste tutorial, ou caso você queira fazer algum comentário ou sugestão a respeito do NetBook, mande um e-mail para mac@cin.ufpe.br.