Gráficos Tartaruga
Seymour Papert inventou "Gráficos Tartaruga" como um sistema
para traduzir um seqüência de símbolos em movimentos
de um autômato (a "tartaruga'') em uma visão gráfica;
a idéia original foi promover um objeto programável que criancas
pudessem aprender a pensa-lo geometricamente). Isto se tornou um sistema
ideal para dar uma interpretação geométrica a dinâmica
dos
L-systems. O sistema básico é como segue. Nós
fixamos um "passo de comprimento"
d
para ser a distância
coberta pela tartaruga em um passo. Nós também fixamos 
como um dado ângulo, normalmente 
para algum inteiro n.
Segundo as convenções do FRACTINT, nós fazemos as seguintes definições:
- F:
- Desenha um passo para frente na direção corrente
- +:
-
Muda a direção de
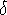no sentido anti-horário
- -:
-
Muda a direção de
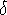no sentido horário
Como um primeiro exemplo do uso destes símbolos, nós introduzimos o L-system da curva de Koch
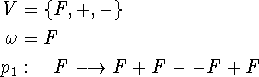
Sem produções específicas mencionadas para alguns
símbolos (neste caso + e -), nós assumimos que eles são
constantes
no sentido que a regra de produção aplicada é 
.
Geração 0 e apenas uma linha reta; nós vamos assumir
que o "cabeçário" no começo está na direção
do eixo horizontal positivo. Nós assumimos o angulo
como 
(na terminologia do FRACTINT , esta conveção esta representada
pela instrução angle=6.Geometricamente,esta produção
significa substituir um segmento de reta F pelo seguinte arranjo
de quatro linhas.
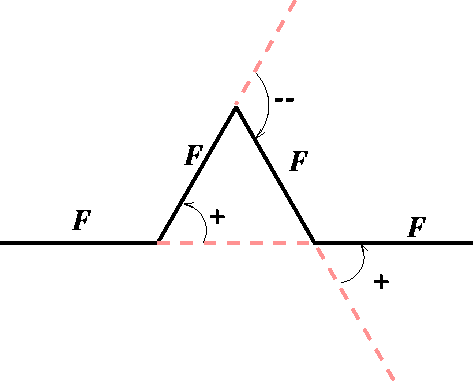
Figura 10: A produção da curva de Koch
Nesta figura, as ações tomadas na travessia do caminho são marcadas pelo símbolo correspondentes em F+F-F+F. Se nós escalonássemos por um fator de três então os pontos inicial e final da curva continuam o mesmo, nós podemos descrever esta produção dizendo que a terceira metade do segmento de reta original foi substituído pela ponta do triângulo equilátero gerado pele terceira metade.
Algumas gerações da curva de Koch estão mostradas abaixo.
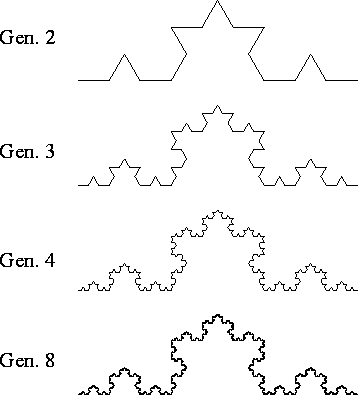
Figura 11: Gerações da curva de Koch
O limite é uma curva fractal do tipo que causou alguma preocupações
entre os matemáticos (Weierstrass e outros) do século dezenove
que estavam trabalhando para construir os rigorosos fundamentos do Cálculo.
Esta curva é um exemplo de uma bijeção continua entre
o intervalo unitário no espaço bidimencional que não
tem uma reta tangente bem definida em qualquer ponto. De fato, a curva
"parece" esta dando voltas de 
ou 
em todos os pontos.
O L-system de Koch cresce rapidamente em termos do número
de segmentos de reta desenhados. Desde que cada segmento de reta é
substituído por outros quatro na proxima geração,
a n-ésima geração tem 
segmentos. Por exemplo, a geração 8 desenhada acima tem 65536
segmentos.
Agora seria o momento oportuno para brincar com as rotinas dos L-systems no FRACTINT. Escolha o tipo fractal para ser "lsystem''. O FRACTINT vai então mostrar um conjunto de definições de L-system, recuperadas de algum arquivo, normalmente fractint.l. Neste arquivo devemos encontrar:
O nome deste L-system, "KochCurve'' (A curva de Kock)
é seguido pelo comentário (comecando com ;) indicando o criador
deste L-system, uma declaração indicando o angulo
é 
, o axioma, e as regras de produções. Depois de digitar a
"ordem" ou geração de números, e pressionando Enter,
FRACTINT mostra a forma resultante.Você pode pressionar a tecla z
para facilmente trocar a ordem, e t para trocar o tipo de fractal.
Voce pode carregar oum utro arquivo de L-systems pressionando a função F6 no PC. Isto faz com que seja possível você criar sua própria definição de um L-system e executá-lo no FRACTINT. Agora nos selecionamos o L-system chamado "Dragon" (Dragão), dado abaixo:
Este é o L-system que gera a curva do Dragão
da secção anterior. O ângulo de incremento é 
. Este L-system tem dois símbolos extra X,Y que não
tem nenhum sentido geométrico, isto é, eles são ignorados
quando é o momento de desenhar a curva desejada. Eles são
ultilizados para assegurar a evolução correta dos comandos
de desenho. Cada segmento de reta desenhado por F é seguido com
um símbolo X ou Y.. Então um segmento FX
é substituído na proxima geração por dois segmentos
de cada tipo com um giro de 
a esquerda entre eles (especificado por ++), enquanto um segmento FY
é substituido por giro a direita. O giro de 
no fim assegura que todos os giros entre FY e FX estão
orientados corretamente. Isto é uma forma elegante de codificação
do processo descrito anteriormente, e isto requer alguma checagem para
verificar que realmente funciona. As primeiras poucas gerações
seguem abaixo:
| Gen. 0 | FX |
| Gen. 1 | -FX++FY- |
| Gen. 2 | -FX++FY-+++FX-FY+- |
| Gen. 3 | --FX++FY-+++FX-FY+-+++-FX++FY--+FX-FY++- |
Mesmo quando o número de + e - entre os segmentos cresce, o giro
é sempre de .
É um exercício interessante desenvolver um L-system
que modifica o sistema do Dragão para que as "pontas" sejam truncadas
suavemente e então nós posssamos facilmente ver o caminho
da curva. Nós vamos ver alguma coisa desta natureza um pouco depois.
